주제
야구 시즌은 팀 간의 경기로 구성되며, 각 경기는 9이닝으로 이루어지고, 한 이닝의 절반은 일련의 타석으로 구성됩니다. 이러한 명확한 구조 덕분에 야구는 비교적 단순한 확률 모델로 표현될 수 있습니다. 이러한 모델을 통한 시뮬레이션은 경기의 다양한 특성을 이해하는 데 도움이 됩니다.
R에서는 다양한 확률 분포에서 시뮬레이션을 할 수 있습니다. 이번에는 R 함수를 사용하여 다수의 타석으로 구성된 경기를 시뮬레이션하는 방법을 보여줍니다.
이번에는 마르코프 체인이라는 특별한 확률 모델을 사용하여 야구 이닝의 절반을 시뮬레이션하는 데 초점을 맞춥니다. 베이스의 주자와 아웃 수가 상태를 정의하며, 이 확률 모델은 3아웃에 도달할 때까지의 상태 간 이동을 설명합니다. 이동 또는 정이 확률은 2016 시즌의 실제 데이터를 사용하여 찾습니다. 이 모델을 사용하여 많은 이닝을 시뮬레이션함으로써 득점 패턴에 대한 기본적인 이해를 얻을 수 있습니다.
하프 이닝 시뮬레이션
마르코프 체인
마르코프 체인은 상태라고 불리는 위치 간의 이동을 설명하는 데 유용한 특별한 유형의 확률 모델입니다. 야구의 맥락에서 상태는 베이스의 주자와 이닝의 아웃 수에 대한 설명으로 볼 수 있습니다. 세 개의 베이스 각각에 주자가 있거나 없을 수 있으므로, 2 × 2 × 2 = 8가지의 가능한 주자 상황이 있습니다. 아웃 수는 세 가지(0, 1, 또는 2)가 가능하므로, 8 × 3 = 24가지의 가능한 주자와 아웃 상태가 있습니다. 3아웃 상태를 포함하면, 야구의 반 이닝 동안 총 25가지의 가능한 상태가 있습니다.
마르코프 체인에서는 전이 확률 행렬을 사용하여 서로 다른 상태 간의 이동을 설명합니다. 예를 들어, 현재 1루와 2루에 주자가 있고 1아웃인 상황을 가정해 봅시다. 타석 결과에 따라 상태가 변할 수 있습니다. 예를 들어, 타자가 안타를 칠 수 있습니다; 2루 주자가 득점하고 1루 주자가 3루로 이동합니다. 이 경우, 새로운 상태는 1루와 3루에 주자가 있고 1아웃인 상황입니다. 또는 타자가 삼진을 당할 수 있고, 새로운 상태는 1루와 2루에 주자가 있고 2아웃인 상황이 됩니다. 전이 확률 행렬의 특정 행을 살펴봄으로써, 1루와 3루에 주자가 있고 1아웃인 상태로 이동할 확률, 또는 1루와 2루에 주자가 있고 2아웃인 상태로 이동할 확률, 또는 다른 가능한 상태로 이동할 확률을 알 수 있습니다.
마르코프 체인에는 두 가지 유형의 상태가 있습니다: 전이 상태와 흡수 상태입니다. 흡수 상태로 이동하면 그 상태에 머물게 되며 다른 전이 상태로 돌아갈 수 없습니다. 야구의 반 이닝에서는 3아웃이 되면 이닝이 끝나므로, 이 3아웃 상태가 흡수 상태 역할을 합니다.
마르코프 체인 모델에는 몇 가지 특별한 가정이 있습니다. 우리는 새로운 상태로 이동할 확률이 현재 상태에만 의존한다고 가정합니다. 따라서 현재의 주자와 아웃 상황 이전에 일어난 야구 이벤트는 확률을 찾는 데 관련이 없습니다. 다시 말해, 이 모델은 이닝을 통해 타격에 모멘텀 효과가 없다고 가정합니다. 또한 우리는 이러한 이동의 확률이 모든 팀, 모든 투수, 그리고 경기 중 모든 이닝에 대해 동일하다고 가정합니다. 분명히, 모든 팀이 평균적이라는 이 가정은 현실적이지 않지만, 우리 는 다음 글에서 이 문제를 다룰 것입니다.
마르코프 체인을 사용하여 야구의 반 이닝을 모델링하는 데는 몇 가지 매력적인 측면이 있습니다. 첫째, 전이 확률 행렬의 구성은 5장의 계산을 사용하여 2016 시즌 데이터로 쉽게 수행할 수 있습니다. 이 모델을 사용하여 많은 반 이닝의 야구를 플레이할 수 있으며, 발견된 득점 패턴은 실제 MLB 야구의 실제 득점과 유사합니다. 마지막으로, 마르코프 체인의 특별한 속성들이 이닝 동안 타석에 들어서는 선수의 수와 같은 흥미로운 계산을 단순화합니다.
득점 기대치(run expectancy)에 대한 연구
마르코프 체인의 전이 행렬을 구성하기 위해서는 다양한 주자/아웃 상태에서 다른 가능한 주자/아웃 상태로의 전이 빈도를 알아야 합니다. 이러한 빈도는 특정 시즌의 Retrosheet 플레이-바이-플레이 데이터를 사용하여 얻을 수 있습니다.
우리는 2016 시즌의 플레이-바이-플레이 데이터를 읽어들이는 것으로 시작하여 retro2016이라는 데이터 프레임을 생성합니다.
library(abdwr3edata)
data("retro2016", package = "abdwr3edata")
다음으로, 우리는 각 야구 경기의 각 반 이닝을 고유하게 식별하기 위해 half_inning_id 변수를 생성합니다. 새로운 변수인 runs는 각 플레이에서 득점한 점수를 나타냅니다. 새로운 데이터 프레임인 half_innings는 2016년에 플레이된 각 반 이닝에 대해 집계된 데이터를 포함합니다.
half_innings <- retro2016 |>
mutate(
runs = away_score_ct + home_score_ct,
half_inning_id = paste(game_id, inn_ct, bat_home_id)
) |>
group_by(half_inning_id) |>
summarize(
outs_inning = sum(event_outs_ct),
runs_inning = sum(runs_scored),
runs_start = first(runs),
max_runs = runs_inning + runs_start
)
dplyr 패키지의 filter() 함수를 사용하여, 우리는 상태가 변하거나 득점 수가 변화하는 플레이에 초점을 맞춥니다. filter()를 다시 한 번 적용하여, 3아웃이 있고 타격 이벤트가 있는 완전한 이닝으로 범위를 제한합니다; 이 새로운 데이터셋을 retro2016_complete라고 부릅니다. 여기서 도루, 도루 실패, 와일드 피치, 패스트볼과 같은 비타격 플레이는 무시됩니다. 득점 생산의 관점에서 이러한 비타격 플레이를 제거하는 것은 분명히 어떤 결과를 초래하며, 이 문제는 나중에 논의됩니다.
retro2016_complete <- retro2016 |>
mutate(
half_inning_id = paste(game_id, inn_ct, bat_home_id)
) |>
inner_join(half_innings, join_by(half_inning_id)) |>
filter(state != new_state | runs_scored > 0) |>
filter(outs_inning == 3, bat_event_fl)
우리가 정의한 new_state 변수에서, 3아웃일 때의 주자 위치를 기록했습니다. 그러나 3아웃 상황에서는 주자 위치가 중요하지 않으므로, 아웃 수가 3일 때 new_state 값을 항상 3으로 재코딩합니다. str_replace() 함수는 정규 표현식 [0-1]{3} 3을 3으로 대체합니다. 이 정규 표현식은 세 개의 이진 문자(0 또는 1)로 이루어진 문자열 뒤에 공백과 3이 오는 패턴을 찾아 대체합니다.
retro2016_complete <- retro2016_complete |>
mutate(new_state = str_replace(new_state, "[0-1]{3} 3", "3"))
전이 확률 계산
이제 state와 new_state 변수가 정의되었으므로, table() 함수를 사용하여 모든 가능한 상태 간 전이의 빈도를 계산할 수 있습니다. 빈도 행렬은 T_matrix입니다. 시작 상태인 state의 가능한 값은 24개이며, 3아웃 상태를 포함한 최종 상태인 new_state의 값은 25개입니다.
T_matrix <- retro2016_complete |>
select(state, new_state) |>
table()
dim(T_matrix)
이 행렬은 prop.table() 함수를 사용하여 확률 행렬로 변환할 수 있습니다. 결과 행렬은 P_matrix로 표시됩니다.
P_matrix <- prop.table(T_matrix, 1)
dim(P_matrix)
마지막으로, 우리는 이 전이 확률 행렬에 3아웃 상태에서의 전이에 해당하는 행을 추가합니다. 이닝이 3아웃에 도달하면 그 상태에 머물러 있으므로, 이 상태에 머물 확률은 1입니다.
P_matrix <- P_matrix |>
rbind("3" = c(rep(0, 24), 1))
이제 P_matrix 행렬은 마르코프 체인에서 상태 간 전이를 모델링할 수 있게 하는 두 가지 중요한 특성을 가지고 있습니다: 1) 정사각 행렬이며; 2) 각 행의 항목들의 합이 1입니다.
dim(P_matrix)
P_matrix |>
apply(MARGIN = 1, FUN = sum)
이 전이 행렬을 더 잘 이해하기 위해, "000 0" 상태(주자 없음, 아웃 없음)에서 시작하는 전이 확률을 아래에 표시합니다. (양의 확률만 표시되며, as_tibble()과 pivot_longer() 함수를 사용하여 확률을 세로로 표시합니다.) 가장 가능성 있는 전이는 "주자 없음, 1아웃" 상태로 0.676의 확률과 "1루 주자, 아웃 없음" 상태로 0.235의 확률입니다. "000 0" 상태에서 "000 0" 상태로 이동할 확률은 0.033입니다. 다시 말해, 주자 없고 아웃 없는 상황에서 홈런을 칠 확률이 0.033입니다.
P_matrix |>
as_tibble(rownames = "state") |>
filter(state == "000 0") |>
pivot_longer(
cols = -state,
names_to = "new_state",
values_to = "Prob"
) |>
filter(Prob > 0)
"010 2" 상태, 즉 2루에 주자가 있고 2아웃인 상황에서 시작하는 가능한 전이를 이와 대조해 보겠습니다. 가장 가능성 있는 전이는 "3 아웃"(확률 0.650), "1, 2루에 주자가 있고 2아웃"(확률 0.156), 그리고 "1루에 주자가 있고 2아웃"(확률 0.074)입니다.
P_matrix |>
as_tibble(rownames = "state") |>
filter(state == "010 2") |>
pivot_longer(
cols = -state,
names_to = "new_state",
values_to = "Prob"
) |>
filter(Prob > 0)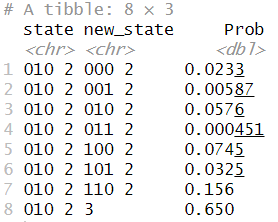
'야구 분석 > R' 카테고리의 다른 글
| R을 이용한 하프 이닝 시뮬레이션 2 (0) | 2024.09.29 |
|---|---|
| 야구 선수들의 정점 나이: 시간에 따른 변화 (0) | 2024.09.09 |
| 메이저리그 선수들의 커리어 살펴보기 (2) | 2024.09.08 |
| 미키 맨틀의 커리어 살펴보기 (0) | 2024.08.22 |
| 포수 프레이밍이란? (0) | 2024.08.14 |